(part 1)
회귀 분석
1. 회귀분석이란
- 독립변수와 종속변수 간 관련성을 설명하는 통계적 모형인 회귀모형을 통해, 두 변수의 데이터로 회귀모형에 적합한 추정회귀식을 계산하고 통계적 분석(추론)을 하는 기법
- 회귀모형의 계수인 "모수"를 추정
- 모수에 대한 구간추정/가설검정 등의 분석
- 종속변수 설명에 있어서 독립변수의 상대적 중요성 평가 가능
- 예) 기업의 시가총액과 투자활동 - 주식 수익률의 관련성 연구
- 과거의 데이터에 의존 (데이터 수집이 중요)
- 과거/현재/미래 예측
2. 회귀분석 종류
- 단순선형회귀분석
- 다중선형회귀분석
- 로지스틱회귀분석
- 비선형회귀분석
2-1. 회귀분석 종류
- 단순선형회귀모형

- 다중선형회귀모형

- 비선형회귀모형

- 다변량회귀모형

단순회귀
1. 단순회귀모형
- 단순선형회귀모형
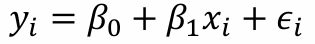
- 추정 단순회귀식

2. 오차항 가정
- E( εi ) = 0, i = 1, ... , n
- 등분산 : Var( εi ) = σ², i = 1, ... , n
- 독립성 : Cov( εi , εj ) = 0, i ≠ j
- 정규성 : εi ~ N( 0, σ² )
3. 종속변수의 분포





4. 최소제곱법
- 어떤 관측값 yi에 대한 오차

- 모든 점에 대한 오차의 제곱합이 최소가 되도록 회귀계수를 추정
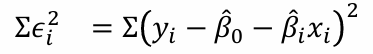
5. 편미분 활용한 최소제곱법의 해

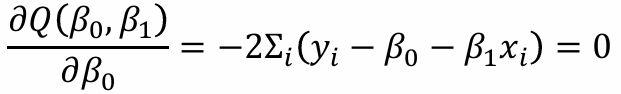
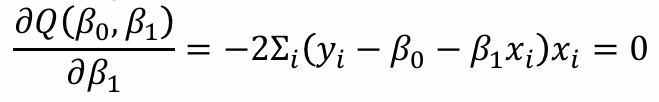
(1), (2)에서 -2를 나눠주고 Σi를 분배한 뒤, (1)에 x̄ = Σxi / n 를 곱해준 뒤, (1) - (2)로 정리하면
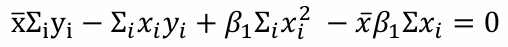
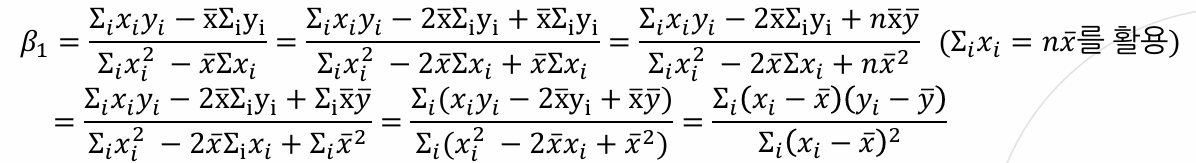
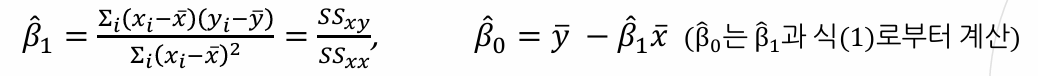
(part 2)
1. 추정 회귀방정식
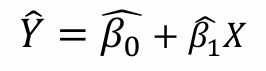
2. 적합값
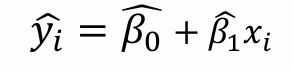
3. 잔차
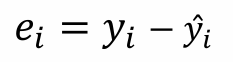
- 잔차의 합은 0
4. 잔차제곱합 (SSE)
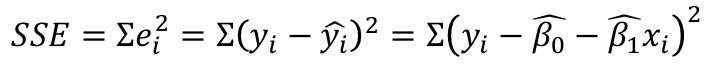
5. MSE
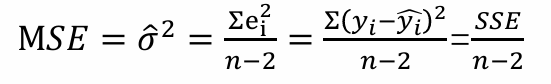
개인첨언 : => 회귀분석에서 잔차 제곱합을 이용해 분산을 추정할 때 (분산의 불편 추정량)
회귀 모델에서 오차의 분산을 추정할 때, 자유도를 고려해 분모를 n - p로 나눈다. p는 회귀계수의 개수
단순 선형 회귀에서는, β0, β1 두 개의 회귀계수를 고려하여 n - 2로 나눔. 따라서 잔차 제곱합을 통해 오차의 분산을 불편하게 추정할 때는 분모에 n - 2를 사용함.
- 오차분산의 불편추정량
- 오차분산 추정시 MSE 사용
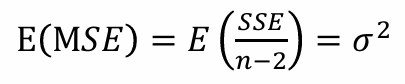
6-1. β1의 추정 및 검정
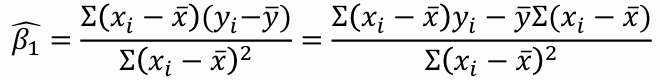
이 때, 분자의 Σ( xi - x̄ )는 편차의 합이므로 0이 됨. 따라서,
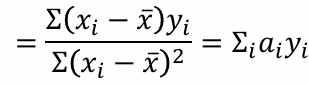
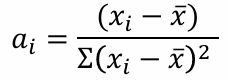
의 몇 가지 특징( (1), (2), (3) )을 활용하여 회귀계수 추정값의 기댓값/분산 계산 가능
(1)
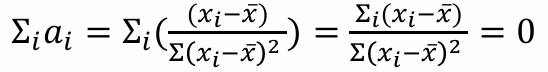
(2)
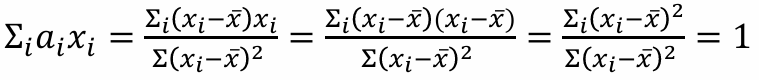
(3)
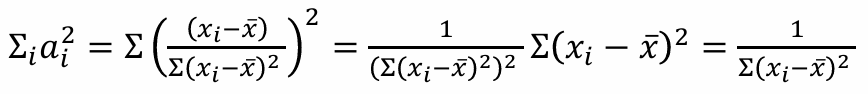
ai의 (1), (2) 특징을 활용하면 아래와 같이 기댓값을 구할 수 있음
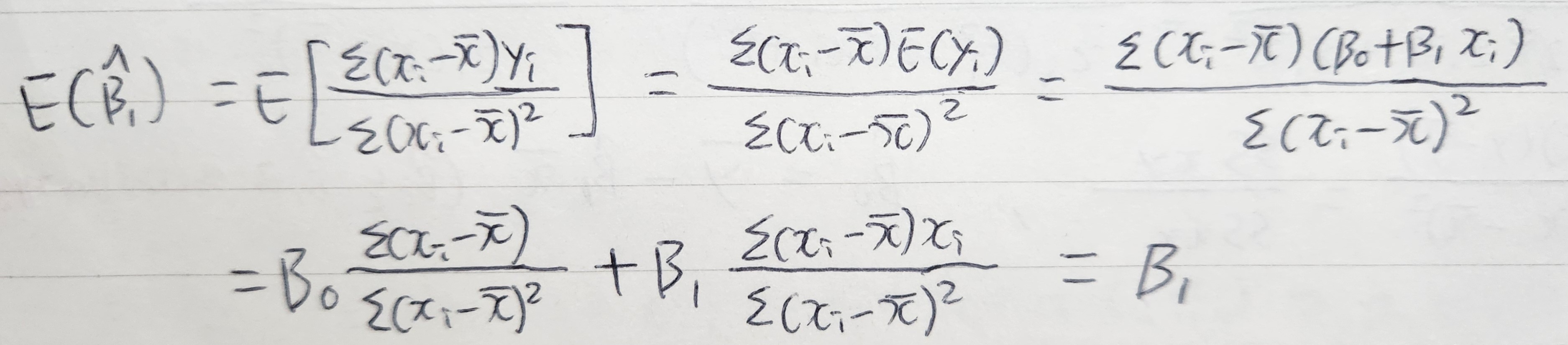
=
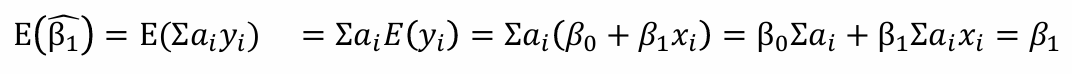
ai의 (3) 특징을 활용하면 아래와 같이 분산을 구할 수 있음
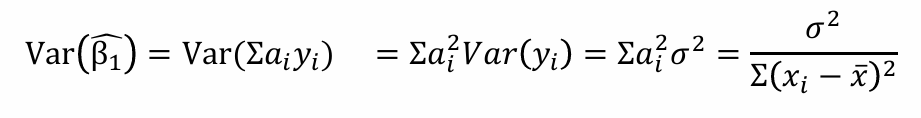
=
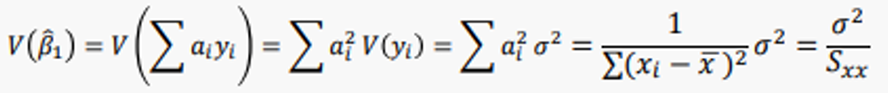
그런데,

개인첨언 : 왜냐하면 MSE의 기댓값이 σ²이라서
이제, 기댓값도 구하고 분산도 구했기 때문에, Beta 1 Hat의 S.E를 사용하면 표준화가 가능. 따라서 검정 가능
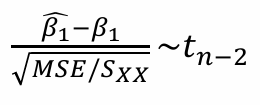
β1의 100(1 - α)% 신뢰구간
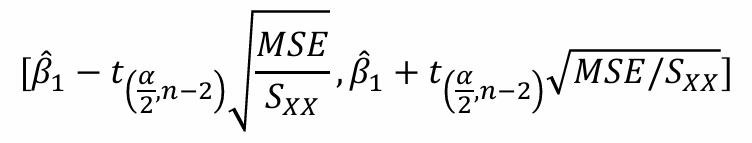
- 검정통계량
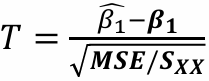
- 양측검정
H0 : β1 = 0, H1 : β1 ≠ 0
- 단측검정
H0 : β1 = 0, H1 : β1 > 0
- 귀무가설 기각 : β1이 0이 아니다. 즉, 독립변수 X는 종속변수에 대해 통계적으로 유의
6-2. β0의 추정 및 검정
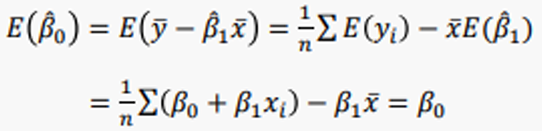
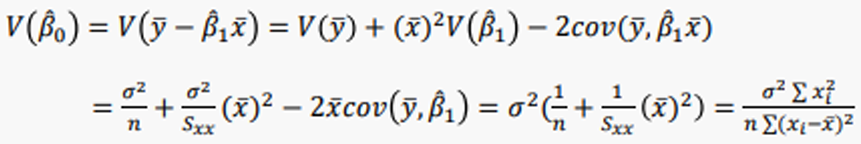
(참고)
β0추정량의 분산을 구할 때, cov를 설명하기 위해, 다음 수식을 보여주겠다.
편의상 ai와 ci를 단축어로써 사용하면,
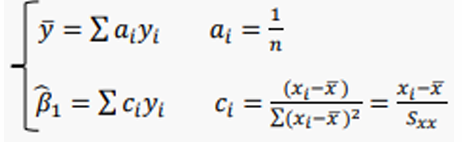
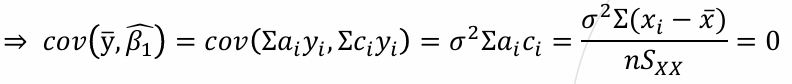
yi 가 독립이기 때문에 cov()의 결과를 이렇게 정의할 수 있다.
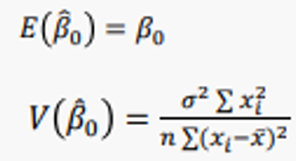
를 통해,
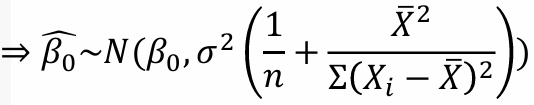
만약 오차분산 σ²을 모른다면
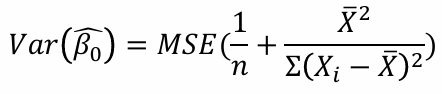
β0의 100(1 - α)% 신뢰구간

- 검정통계량
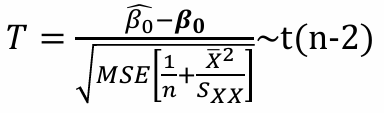
강의는 통계수학 기초에 관한 내용을 다루고 있으며, 강의를 복습하기 위해 블로그에 다시 한 번 요약정리 하고 있다. 강의에서는 더욱 자세한 내용 설명과 예제를 통한 수학적 증명을 설명해주고 있으니, 통계수학에 대한 공부를 하고 싶은 사람은 꼭 이 강의를 수강하길 강추한다.
공부내용 :
https://www.metacodes.co.kr/edu/read2.nx?M2_IDX=30098&page=1&sc_is_discount=&sc_is_new=&EP_IDX=8382&EM_IDX=8208
통계 기초의 모든것 올인원 [ 1편, 2편 ]ㅣ18만 조회수 검증
www.metacodes.co.kr
'[통계학]' 카테고리의 다른 글
| 회귀분석 (2) (3) | 2024.10.24 |
|---|---|
| 분산 분석 - 일원배치 / 이원배치 (3) | 2024.10.23 |
| 두 모집단 비교 - 두 모집단 비교 / 두 모평균 비교 / 대응비교 / 두 모비율 비교 / 두 모분산 비교 (2) | 2024.10.22 |
| 검정 - 검정의 요소 알아보기 / 검정력 함수 / 검정 절차 / 모평균검정 / 모비율검정 / 모분산검정 (3) | 2024.10.22 |
| 추정 - 점추정 / 구간추정 / (모평균,모비율,모분산의) 구간추정 / 표본크기결정 (1) | 2024.10.21 |