분산 분석
1. 분산분석(Analysis of Variance)
- 독립변수의 수준(범주)으로 나뉜 집단 간 평균 차이를 검정
- 특정값의 산포를 인자별로 분해하여 어느 인자가 큰 영향을 주는지
- 반응변수
- 처리(treatment)에 의해 변화하는, 연구대상이 되는 변수
- 인자(= 요인, factor)
- 반응변수에 영향을 주는 변수
- 독립변수, 설명변수
- 처리(treatment)
- 요인의 특정 값(특정 실험 조건)
- 수준(level)
2. 기본 가정
- 각 집단의 모집단 분포는 정규분포
- 각 집단의 모집단의 분산 같음
- 각 모집단 내의 오차와 모집단 간 오차는 독립
3. 분산분석(Analysis of Variance) 분해
- 전체 변동 = 그룹 간 변동 + 그룹 내 변동
- 그룹 간 변동 = 요인에 의한 효과
- 그룹 내 변동 = 오차에 의한 효과
- 그룹 간 분산과 그룹 내 분산의 비교
4. 종류
- 일원배치 분산분석 (one-way anova)
- 2 sample t test와 같은 목적이지만 anova는 2개 이상의 모집단의 평균 비교
- 인자가 하나인 경우, 두 개 이상의 모집단 평균이 서로 동일한지 검정
- 이원배치 분산분석 (two-way anova)
- 인자가 두 개인 경우에 사용
- 인자의 수준 및 교호 작용에 의한 영향 파악 가능
분산 분석 - 일원배치
1. 일원배치 분산분석
- 한 개의 요인
- 가정
- k(treatment의 가짓 수)개의 모집단은 독립 & 정규분포
- 각 집단의 모집단 평균은 서로 다를 수 있으나 분산은 같음
2. 가설검정
H0 : μ1 = μ2 = ... = μk
H1 : 적어도 하나의 평균은 다르다
1-1. 일원배치 분산분석 - 반복수(특정 처리를 가하면 그룹 안의 인원수가 몇 개)가 같은 경우 (=> 집단 별 인원이 같다)

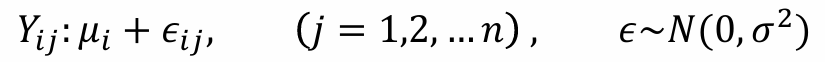
개인첨언 : Yij = 특정 처리집단의 모평균 + 오차항(개별관측값이 가질 수 있는)
오차항 => 평균은 0이고 입실론(오차항)들 간의 분산은 동일
1-2. 관찰값 모형

μ : 전체 모평균
μi : i번째 처리의 모평균
αi : 처리 i의 효과, 처리 i에서의 모평균 μi가 전체 모평균 μ로부터 어느정도 치우쳤는지 - Σαi = 0
εij : i번째 처리의 j번째 반응값이 가지는 오차, 상호 독립, εij ~ N(0, σ²)
오차항의 가정
1) 정규성 : 정규분포
2) 독립성 : 오차항 간 독립
3) 비편향성 : 기댓값은 0 (Bias 없음)
4) 등분산성 : 모든 오차항의 분산 동일
개인첨언 : 잔차진단 => 분석모형이 오차항의 가정을 모두 만족시키는지에 대해 test
1-3. 귀무가설 수립
H0 : μ1 = μ2 = ... = μk --> H0 : α1 = α2 = ... = αk
1-4. 제곱합 분해
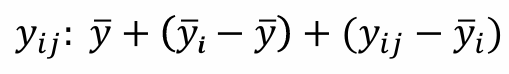
1) ( y̅i - y̅ ) : i번째 집단의 평균과 전체평균 간의 차이 = 처리효과의 크기
2) (yij - y̅i ) : 각 관찰값과 각 집단평균 간의 차이 = 잔차

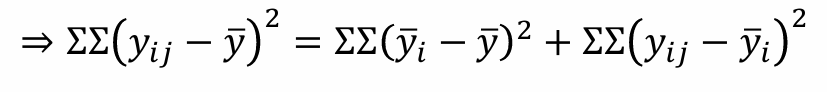
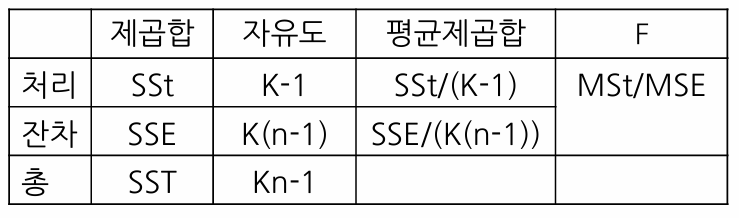
- 제곱합 : SST = SSt + SSE
- (총 분산) = (처리 간 분산) + (처리 내 분산)
- 자유도 : kn - 1 = (k - 1) + k(n - 1)
1-5. 평균 제곱
- 제곱합을 자유도로 나눈 값 (분산의 추정량)
- MSt (처리평균제곱)

- MSE (잔차평균제곱)
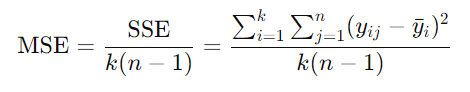
- F-통계량
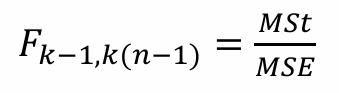
1-6. ANOVA Table
1-7. 가설검정 (반복수 같음)
- 각 처리 집단의 평균이 같다면 SSt는 작아짐 (SSE 커짐)
- 각 처리 집단의 평균이 다르다면 SSt는 커짐 (SSE 작아짐)
H0 : α1 = α2 = ... = αk
- 검정통계량 F = MSt / MSE
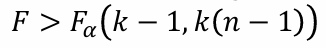
-> 귀무가설 기각
1-8. 독립변수의 설명력
- 상관비 지수

- 독립변수의 설명력을 나타냄
1-9. 사후검정
- 어떤 집단 간에서 유의한 차이가 발생했는지 사후적으로 분석
- Post hoc comparison
- LSD, TUKEY, DUNCAN 등
2. 일원배치 분산분석 - 반복수가 다른 경우


2-1. 관찰값 모형 - 반복수 다름

μ : 전체 모평균
μi : i번째 처리의 모평균
αi : 처리 i의 효과, 처리 i에서의 모평균 μi가 전체 모평균 μ로부터 어느정도 치우쳤는지

εij : i번째 처리의 j번째 반응값이 가지는 오차, 상호독립, εij ~ N(0, σ²)
2-2. 제곱합 분해

1) ( y̅i - y̅ ) : i번째 집단의 평균과 전체평균 간의 차이 = 처리효과의 크기
2) ( yij - y̅i ) : 각 관찰값과 각 집단평균 간의 차이 = 잔차
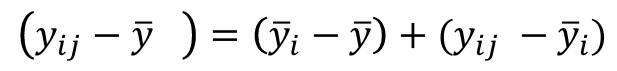

- 제곱합 : SST = SSt + SSE
- (총 분산) = (처리 간 분산) + (처리 내 분산)
- 자유도 : kn - 1 = (k - 1) + k(n - 1)
2-3. ANOVA Table
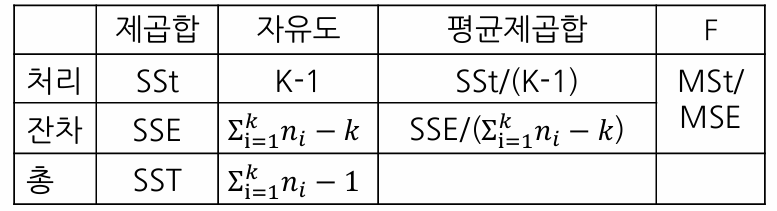
2-4. 가설검정 (반복수 다름)
- 각 처리 집단의 평균이 같다면 SSt는 작아짐 (SSE 커짐)
- 각 처리 집단의 평균이 다르다면 SSt는 커짐 (SSE 작아짐)
H0 : α1 = α2 = ... = αk
- 검정통계량 F = MSt / MSE

-> 귀무가설 기각
분산 분석 - 이원배치
1. 이원배치 분산분석 (반복 X)
- 두 개의 요인 (A, B)
- 요인 A (수준 p개)
- 요인 B (수준 q개)
1-2. 가설검정
H0 : μA1 = μA2 = ... = μAp
μB1 = μB2 = ... = μBq
H1 : 적어도 요인 A 하나의 평균은 다르다
적어도 요인 B 하나의 평균은 다르다
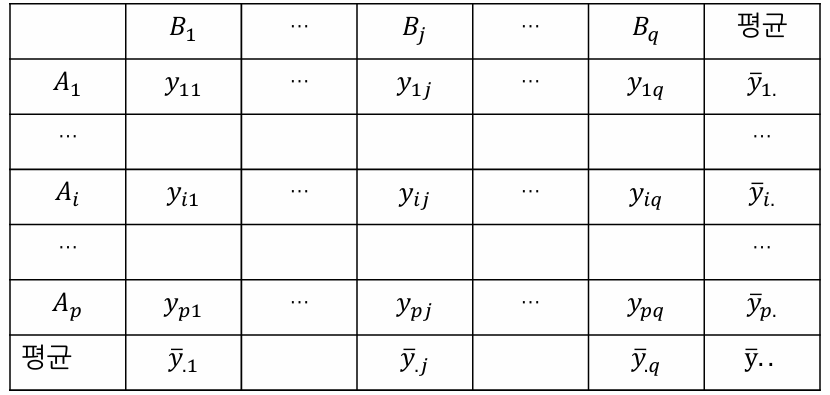
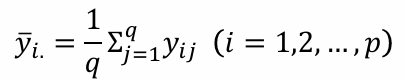


1-3. 관찰값 모형

μ : 전체 모평균
αi : A의 i번째 수준 효과 - Σαi = 0
βj : B의 j번째 수준 효과 - Σβj = 0
εij : 오차항, 상호독립, εij ~ N(0, σ²)
1-4. 귀무가설 수립
H0 : μA1 = μA2 = ... = μAp => H0 : α1 = α2 = ... = αp
μB1 = μB2 = ... = μBq => H0 : β1 = β2 = ... = βq
1-5. 제곱합 분해





1-6. ANOVA Table
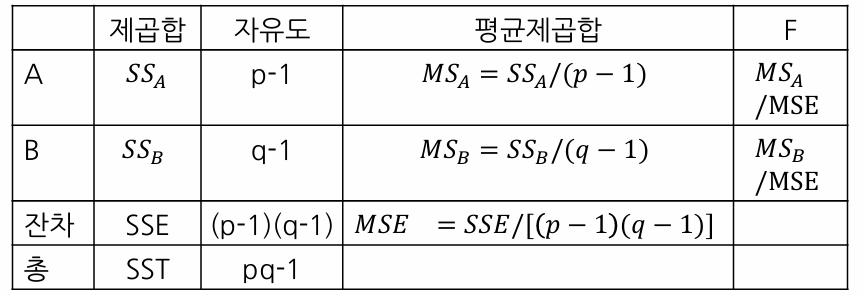
1-7. 가설검정
H0 : α1 = α2 = ... = αp
- 검정통계량 F = MSA / MSE
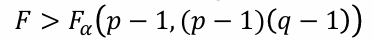
-> 귀무가설 기각
2. 이원배치 분산분석 (반복 O)
- 두 개의 요인 (A, B)
- 요인 A (수준 p개)
- 요인 B (수준 q개)
- 주 효과 분석
- 독립변수 개별 효과 분석
- 상호작용 효과
- 주 효과들 간 교호작용 분석
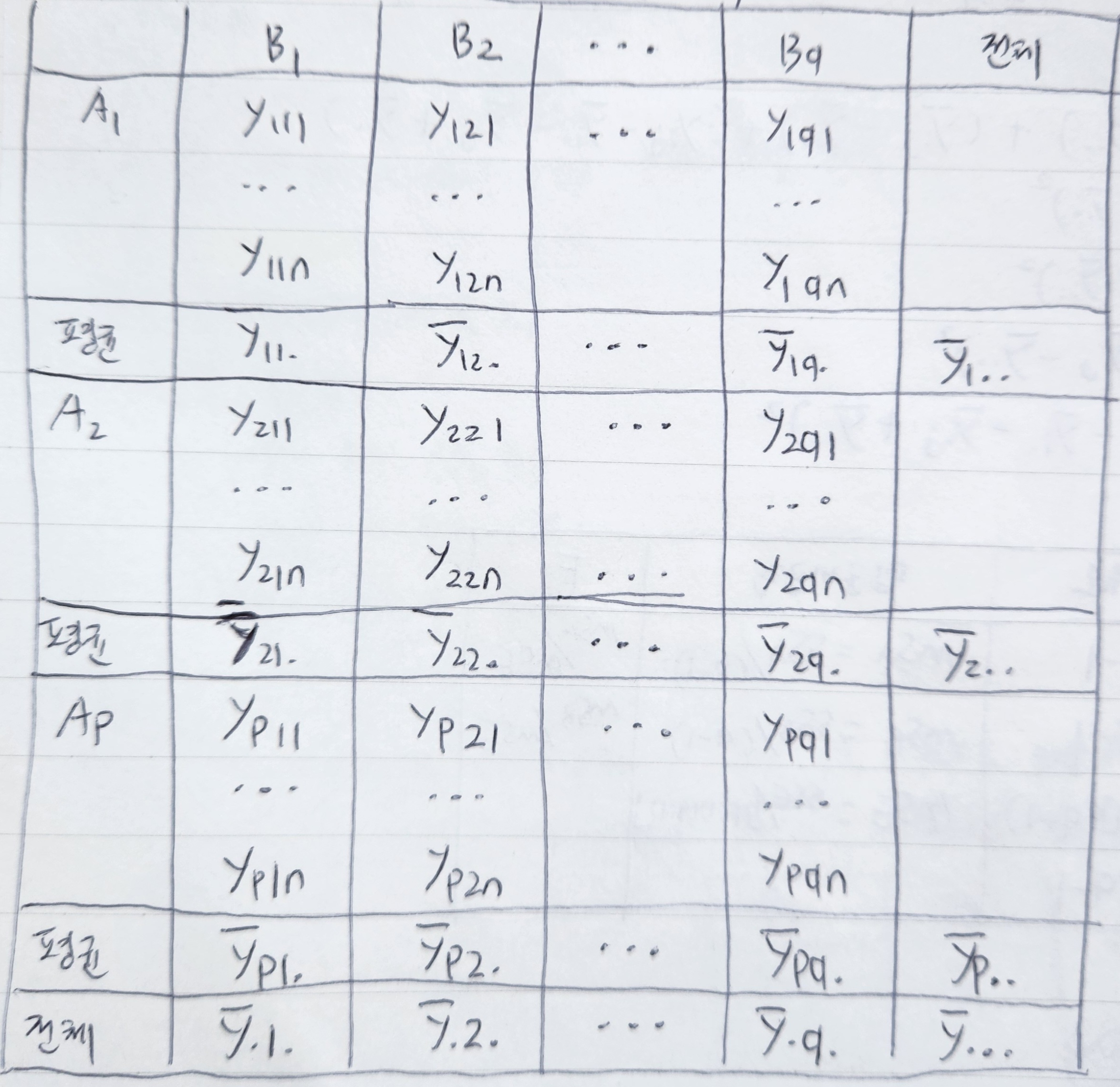
2-1. 관찰값 모형
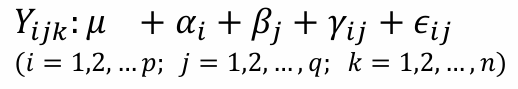
μ : 전체 모평균
αi : A의 i번째 수준 효과 - Σαi = 0
βj : B의 j번째 수준 효과 - Σβj = 0
γij : A(i)와 B(j)의 교호작용 효과
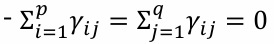
εij : 오차항, 상호독립, εij ~ N(0, σ²)
2-2. 귀무가설 수립
H0 : α1 = α2 = ... = αp
H0 : β1 = β2 = ... = βq
H0 : γij = 0
2-3. 제곱합 분해
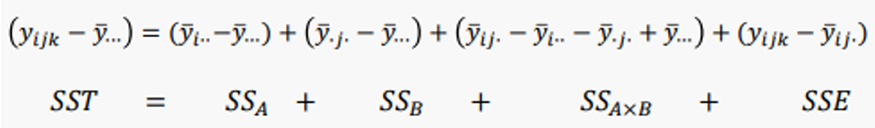
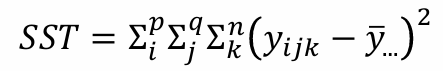

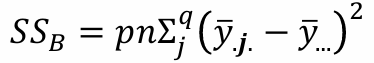

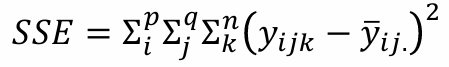
2-4. ANOVA Table

2-5. 가설 검정
H0 : α1 = α2 = ... = αp
- 검정통계량 F = MSA / MSE

-> 귀무가설 기각
H0 : γij = 0
- 검정통계량 F = MSA,B / MSE
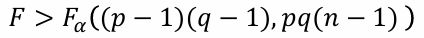
-> 귀무가설 기각
2-6. 독립변수의 설명력
- A의 설명력
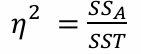
- B의 설명력
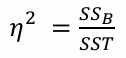
- 교호작용 설명력

- A, B, AB 상호작용 설명력
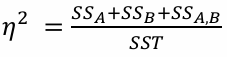
- 오차분산의 비율
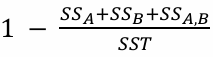
개인첨언 : 총 변동 중에서 설명되지 않은 변동의 비율(= 오차분산의 비율)
강의는 통계수학 기초에 관한 내용을 다루고 있으며, 강의를 복습하기 위해 블로그에 다시 한 번 요약정리 하고 있다. 강의에서는 더욱 자세한 내용 설명과 예제를 통한 수학적 증명을 설명해주고 있으니, 통계수학에 대한 공부를 하고 싶은 사람은 꼭 이 강의를 수강하길 강추한다.
공부내용 :
https://www.metacodes.co.kr/edu/read2.nx?M2_IDX=30098&page=1&sc_is_discount=&sc_is_new=&EP_IDX=8382&EM_IDX=8208
통계 기초의 모든것 올인원 [ 1편, 2편 ]ㅣ18만 조회수 검증
www.metacodes.co.kr
'[통계학]' 카테고리의 다른 글
| 회귀분석 (2) (3) | 2024.10.24 |
|---|---|
| 회귀분석 (1) (3) | 2024.10.24 |
| 두 모집단 비교 - 두 모집단 비교 / 두 모평균 비교 / 대응비교 / 두 모비율 비교 / 두 모분산 비교 (2) | 2024.10.22 |
| 검정 - 검정의 요소 알아보기 / 검정력 함수 / 검정 절차 / 모평균검정 / 모비율검정 / 모분산검정 (3) | 2024.10.22 |
| 추정 - 점추정 / 구간추정 / (모평균,모비율,모분산의) 구간추정 / 표본크기결정 (1) | 2024.10.21 |