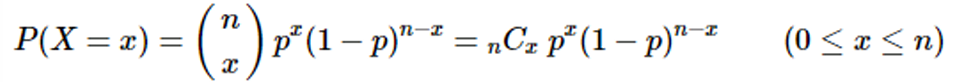인동머스크

이산확률분포 : 이항분포1. 베르누이 시행사상이 두 개뿐인 시행(성공 or 실패)각 시행에서 성공확률과 실패확률의 합은 1각 시행은 서로 독립베르누이 시행을 n번 독립시행 했을 때의 확률변수 x의 분포는 이항분포x01f(x)1 - pp이 때, 확률변수 X의 평균(기댓값) : p확률변수 X의 분산 : p(1 - p)  2. 이항확률분포베르누이 시행을 반복하여 특정한 횟수의 성공/실패가 나타날 확률 3. 이항확률분포의 확률질량함수n : 시행 횟수, x : 성공 횟수, p : 성공 확률기댓값 : np분산 : np(1 - p)  포아송분포1. 포아송분포단위시간, 단위공간 내 발생하는 사건의 횟수를 확률변수 X라고 할 때, X는 λ를 모수로 갖는 포아송분포 따름발생빈도가 낮은 사건의 단위 당 발생 수 2. 포아송..

확률과 확률변수 : 확률 정의1. 표본공간(S) : 랜덤한 현상의 모든 가능한 결과의 집합2. 사건(event) : 표본공간의 부분집합합사상 A∪B곱사상 A ∩ B여사상 Ac배반사상 A ∩ B=∅3. Flipping Coin Twice표본공간 S : {HH, HT, TH, TT}사건 A : 동전을 두 번 던지는 시행에서 동전의 앞면이 1번만 A = {HT, TH}  4. 확률의 고전적 정의 : 가능한 결과가 N가지이고, 각 결과가 나타날 가능성이 모두 같을 때, 사건 A에 속하는 결과가 m개라면 A의 확률 5. 경험적 정의(상대도수) 6. 확률의 공리적 정의 : 표본공간 S에서의 임의의 사상 A에 대하여,0 P(S) = 1서로 배반인 사상들에 대하여이 때, P(A)를 사상 A의 확률이라고 함  7. 확률..

1. 통계통계는 데이터의 수집, 분석, 추론, 요약 등의 방법론을 다룬다.(The art and science of learning from data)Design(설계/계획)Description(요약) : 데이터를 요약 표현하기 위한 시각적(Graphical), 수치적(numerical) 방법Inference(추론) : 표본에 기반한 모집단에 대한 추론/예측  모집단(Population) : 통계학에서 관심/조사의 대상이 되는 개체의 전체 집합모수(Parameter) : 모집단에 대한 수치적 요약고등학생의 1일 평균 온라인게임 플레이시간강아지보다 고양이를 좋아하는 성인의 비율표본(Sample) : 모집단을 적절히 대표하는 모집단의 일부통계량(Statistic) : 표본에 대한 수치적 요약고등학생 1000..