통계검정 : 가설
1. 가설 검정
설정한 가설이 옳을 때 표본에서의 통계량과 통계량의 분포에서 이론적으로 얻는 특정 값을 비교하여 가설의 기각/채택 여부를 판정하는 방법
확률적 오차 범위를 넘어서면 가설을 기각한다.
유의수준(α) : 기각/채택 여부의 판단기준
2. 가설의 종류
귀무가설(H0)
- 대립가설과 상반되는 가설로, 일반적인 사실을 귀무가설로 설정
- 효과가 없다, 차이가 없다 등의 내용
대립가설(H1)
- 입증하고자 하는 가설
- 효과가 있다, 차이가 있다 등의 내용
오류
1. 가설설정의 오류
- 제 1종 오류(α)
- 귀무가설을 채택해야 했음에도 이를 기각할 오류
- 표본으로부터 얻은 검정결과가 우연에 의해 귀무가설을 기각하도록 오판된 가능성
- α는 일반적으로 5%로 설정
- 제 2종 오류(β)
- 귀무가설을 기각해야 했음에도 이를 채택할 오류
- 실제로는 효과가 있는데 효과가 없다고 잘못 결론 내릴 가능성
- β는 일반적으로 10%로 설정
요소
1. 유의수준(significance level)
제 1종 오류를 범할 확률의 최대 허용 한계
2. 유의확률(p-value)
- 검정통계량 값에 대해 귀무가설을 기각할 수 있는 최소의 유의수준으로 귀무가설이 참일 때 관측된 검정통계량 이상의 극단적인 결과가 발생할 가능성
- α > p-value : 귀무가설 기각
- α < p-value : 귀무가설 기각하지 않음
개인 첨언 : α > p-value : p-value가 작다는 것은 관측된 데이터가 귀무가설 하에서 매우 드문 일이 발생했음을 의미. 귀무가설이 참이라고 가정할 때 이런 극단적인 결과가 나올 가능성이 유의수준 이하라는 뜻. 그래서 귀무가설 기각. 유의수준이 0.05일때, p-value가 0.03이면 귀무가설이 참일 때 이러한 결과가 나올 확률이 3%밖에 되지 않으므로, 귀무가설을 기각할만한 충분한 증거가 있다고 판단.
α < p-value : p-value가 유의수준보다 크면 관측된 결과가 귀무가설 하에서 흔히 발생할 수 있는 범위 내에 있다는 뜻. 이런 경우에는 귀무가설을 기각할 충분한 증거가 없다고 보고 귀무가설을 기각하지 않음.
3. 임계값(critical value)
- 기각역과 채택역을 나누는 경계값
- 기각역 : 귀무가설을 기각하게 되는 검정통계량의 관측값의 영역
- 채택역 : 귀무가설을 채택하게 되는 검정통계량의 관측값의 영역
- 검정통계량의 관측값이 기각역에 속하면 귀무가설 기각
절차
1. 검정할 가설을 설정
2. 유의수준을 설정
3. 임계치를 결정하고 검정통계량과 임계치를 비교 (혹은 유의수준과 유의확률 비교)
4. p-value 값이 유의수준보다 작으면 귀무가설을 기각
양측검정과 단측검정
1. 양측검정(Two-sided)
- 기각역이 각각 왼쪽과 오른쪽 두 부분으로 구성된 가설검정
- 양쪽 기각역의 합 = 유의수준

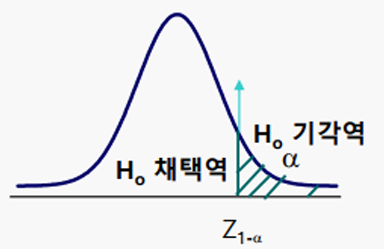
2. 단측검정(One-sided)
- 기각역이 한 쪽으로만 구성되는 가설검정
- 한 쪽 기각역이 유의수준
모평균 검정
1. 정규모집단의 경우
1) 모분산이 알려진 경우 : Z 검정 통계량

2) 모분산을 모르는 경우 : t 검정 통계량(자유도 n - 1)

2. 표본 크기가 큰 임의의 모집단
1) 모분산이 알려진 경우 : Z 검정 통계량

2) 모분산을 모르는 경우 : Z 검정 통계량

강의는 통계수학 기초에 관한 내용을 다루고 있으며, 강의를 복습하기 위해 블로그에 다시 한 번 요약정리 하고 있다.
강의에서는 더욱 자세한 내용 설명과 예제를 통한 수학적 증명을 설명해주고 있으니, 통계수학에 대한 공부를 하고 싶은 사람은 꼭 이 강의를 수강하길 강추한다.
공부내용 :
통계 기초의 모든것 올인원 [ 1편, 2편 ]ㅣ18만 조회수 검증
www.metacodes.co.kr
'[통계학]' 카테고리의 다른 글
| 추정 - 점추정 / 구간추정 / (모평균,모비율,모분산의) 구간추정 / 표본크기결정 (1) | 2024.10.21 |
|---|---|
| 표본분포 - 표본분포 / 중심극한정리 / 카이제곱분포 / t분포 / F분포 (0) | 2024.10.21 |
| 통계적 추정 - 통계적 추정의 정의와 기준 / 점추정 / 구간추정 / 모분산 아는경우 / 모분산 모르는 경우 (0) | 2024.10.21 |
| 연속확률분포 - Uniform Distribution / 정규분포 / 표본분포 / 중심극한정리 / 카이제곱분포 / t분포 및 F분포 (0) | 2024.10.20 |
| 이산확률분포 - 이항분포 / 포아송분포 (0) | 2024.10.20 |