이번 8회 빅데이터 분석기사 필기/실기 시험은 메타코드 온라인 강의를 수강하여 대비하기로 결정하였다.
메타코드는 데이터사이언스와 인공지능을 비롯한 전반적인 데이터 직무에 대한 교육을 받을 수 있는 교육 사이트이다.
메타코드에서 서포터즈를 뽑는다는 공지를 보고 데이터분석 직무에 대한 공부를 하겠다는 마음가짐과 성실성을 어필하게 되었고,
좋은 기회를 받아 이번 5기 서포터즈에 합류하게 되었다.
메타코드 서포터즈 첫 활동으로, 2024 빅분기 실기 강의에 대한 내용의 일부와 그 후기를 작성하고자 한다.
3. 회귀분석
1) 다중선형회귀 (LinearRegression)
독립변수(X)가 종속변수(Y)에 어떻게 영향을 주는지 식으로 표현한 것
*특징 : 식을 보고 설명이 가능함, 가장 적은 수의 X로 Y를 잘 예측하는게 Best

단순선형회귀(독립변수가 1개)
Y = β0 + β1X
다중선형회귀(독립변수가 2개 이상)
Y = β0 + β1X1 + β2X2 ...

Σ(y - ŷ)² (= RSS = SSE) 값이 최소가 되는
최적의 β0, β1 를 구하면 된다.
-> 최소제곱법이라고 부름
*RSS : Residual Sum of Squares
■ 회귀식의 성능
1. 결정계수(R²) : 0 ~ 1 사이의 값을 가짐
- 정의 : 전체 변동에서 회귀식이 설명 가능한 변동의 비율
R² = SSR / SST = 1 - (SSE / SST)

SSR : 회귀식에 의해 설명되는 변동
SSE : 회귀식으로 설명 불가한 변동
SST : 총 변동(SSR + SSE)

2) 로지스틱 회귀분석 (LogisticRegression)
1. 종속변수(Y)가 범주형(이진형으로 0과 1)인 경우에 사용할 수 있는 회귀분석
2. 독립변수(X)를 가지고 Y = 1 일 확률이 얼마인지 예측하는 모형
(확률이 0.5보다 크면 1로, 0.5보다 작으면 0으로 분류)
■ 로지스틱 함수 적용(= Sigmoid 함수)

■ Odds(승산)의 정의
odds = P / 1 - P = 성공할 확률(Y=1) / 실패할 확률(Y=0)
예시 ) 성공할 확률 0.75, 실패할 확률 0.25이면 성공할 확률이 실패할 확률보다 3배 크다 (odds = 3)
■ Logit과 Odds (로짓과 오즈)

*Logit : odds에 자연로그를 취한 값
■ 회귀계수의 해석
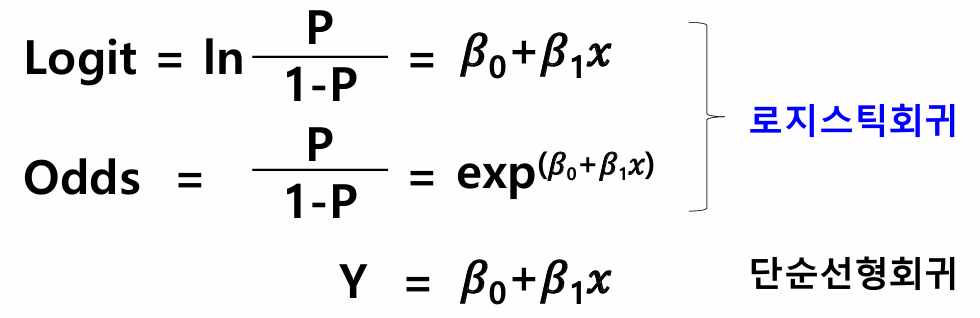
- 단순(다중)선형회귀에서 x가 1단위 올라가면 -> Y는 기존 대비 β1 만큼 증가
- 로지스틱 회귀에서 x가 1단위 올라가면 -> odds는 기존대비 exp^(β1) 만큼 증가
여기서 exp^(β1)를 odds ratio 라고 함(odds 변화량)
■ 최적의 파라미터(회귀계수)를 구하려면
선형회귀
Y = β0 + β1X1
∑(y - ŷ)² (= RSS = SSE) 값이 최소가 되는 최적의 β0, β1를 구하면 된다.
-> 최소제곱법이라고 부름
*RSS : Residual Sum of Squares
로지스틱회귀
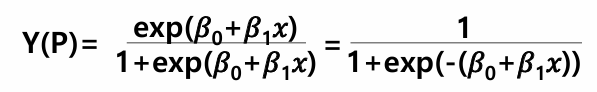
*Y는 Class가 1일 확률(P)
Cross Entropy가 최소가 되는 최적의 β0 , β1를 구하면 된다.
(= Log likelihood Function이 최대가 되는)
= Cross Entropy , Residual deviance를 최소가 되게
= Log likelihood Function을 최대가 되게
*Residual deviance = 2 * Cross Entropy
■ Cross entropy 이해하기 (1/2)
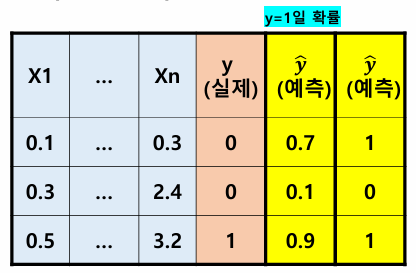
- 분류(Classification)
: Y(종속변수)가 범주형
- 정확도, 민감도(재현율)
- 특이도, F1 Score
- Cross entropy
- Cross entropy
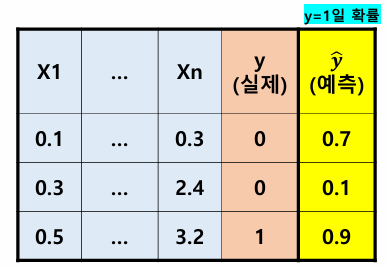
핵심 Concept : 실제값 y와 예측값 ŷ의 차이가 작으면 된다.
y = 1일 때 ŷ(P)값이 작아질수록 Error 값을 크게 주고
y = 0일 때 ŷ(P)값이 커질수록 Error 값을 크게 주자.
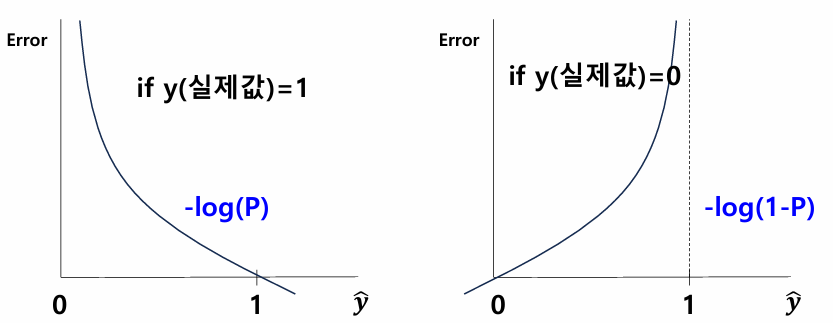
정리하면
y = 1일 때 -log(P) 가 최소
y = 0일 때 -log(1-P) 가 최소
Cross entropy
→ Σ-ylog(P) - (1-y)log(1-P)
y=1일때 y=0일때
■ Cross entropy 이해하기 (2/2)
Σ-ylog(P) - (1-y)log(1-P)
y=1일때 y=0일때
계산해보기
-log(P) -(1-y)log(1-P) = -log(0.3)
-log(P) -(1-y)log(1-P) = -log(0.9)
-log(P) -(1-y)log(1-P) = -log(0.9)
*알아두기
1) Cross Entropy(Log loss) = - Log likelihood Function
2) Cross Entropy * 2 = Residual deviance (잔차 이탈도)
이번 강의에서는 실기 3유형의 핵심 이론인 다중회귀분석과 로지스틱회귀분석을 공부하였다.
각 분석에 대한 내용을 충분히 이해할 수 있게 여러가지 그래프를 보여주며, 그 특성과 분석지표에 대한 설명을 구체적으로 잘 들을 수 있었다.
다음부터 이어진 강의는 지금까지 배웠던 3유형 이론들을 코드를 이용해 실습해 보는 시간, 실제 3유형 예상 모의고사에 대한 풀이가 진행될 것이다.
하지만 다음강의부터 진행될 내용은 이 수강후기 블로그에서 다루지 않을 것이다.
만약 궁금하시다면 다음 빅데이터 분석기사 9회, 10회 실기시험을 메타코드 강의를 통해 대비해 보시길 바란다.
그만큼 직접 수강을 하며 들어야 할 가치가 있는 강의이다.
24년 빅분기 (필기+실기 Python) 최단기 합격패스
www.metacodes.co.kr
'[데이터자격시험용-필수요약정리]' 카테고리의 다른 글
| [2024 빅분기 실기] 메타코드 강의 후기 | 3유형 (5) - 상관분석 (0) | 2024.06.19 |
|---|---|
| [2024 빅분기 실기] 메타코드 강의 후기 | 3유형 (4) - 카이제곱검정 (0) | 2024.06.18 |
| [2024 빅분기 실기] 메타코드 강의 후기 | 3유형 (3) - 모평균검정 (2) | 2024.06.17 |
| [2024 빅분기 실기] 메타코드 강의 후기 | 3유형 (2) (0) | 2024.06.16 |
| [2024 빅분기 실기] 메타코드 강의 후기 | 3유형 (1) (2) | 2024.06.16 |