이번 8회 빅데이터 분석기사 필기/실기 시험은 메타코드 온라인 강의를 수강하여 대비하기로 결정하였다.
메타코드는 데이터사이언스와 인공지능을 비롯한 전반적인 데이터 직무에 대한 교육을 받을 수 있는 교육 사이트이다.
메타코드에서 서포터즈를 뽑는다는 공지를 보고 데이터분석 직무에 대한 공부를 하겠다는 마음가짐과 성실성을 어필하게 되었고,
좋은 기회를 받아 이번 5기 서포터즈에 합류하게 되었다.
메타코드 서포터즈 첫 활동으로, 2024 빅분기 실기 강의에 대한 내용의 일부와 그 후기를 작성하고자 한다.
1. 가설검정 - 모평균 비교(1개)
1. 단일표본 t-test
stats.ttest_1samp(a, popmean=기준값, alternative='two-sided'/'greater'/'less')
모집단의 평균값 vs 기준값
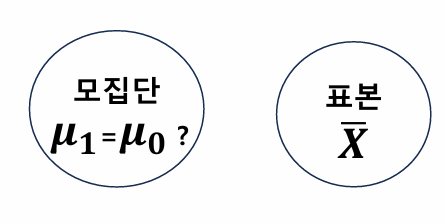
가설설정
H0 : μ1 = μ0 (기준값)
H1 : μ1 != μ0 (기준값)
검정통계량
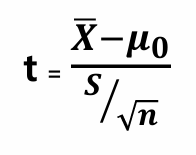
X̄ : 표본평균
μ0 : 기준값
S : 표본표준편차
n : 표본의 크기
1. 가설검정 - 모평균 비교(2개)
2. Paired t-test(쌍체 t-test)
stats.ttest_rel(a, b, alternative='two-sided'/'greater'/'less')

가설설정
H0 : μd = 0
H1 : μd != 0
검정통계량

D(bar) : 차이값들의 평균
Sd : 차이값들의 표준편차
n : 표본의 크기
3. 독립표본 t-test
stats.ttest_ind(a, b, equal_var=True, alternative='two-sided'/'greater'/'less')
등분산 필수 확인(True or False)

가설설정
H0 : μ1 = μ2
H1 : μ1 != μ2
검정통계량 등분산 가정

X̄1, X̄2 : 각 집단 표본평균
Sp ² : 합동 표본분산
Sp : 합동 표본표준편차
n1, n2 : 표본의 크기
- 모분산은 모르지만 표본의 분산이 동일할 경우 합동 표본분산
- 검정통계량은 자유도 (n1+n2 - 2)인 t분포를 따름
(이분산일 경우 합동 표본분산을 사용할 수 없으며, 분포의 자유도도 별도 공식으로 구해야 함)
※ 독립표본 t-test 전체적으로 이해해보기(평균차이, 분산, 검정통계량, p-value, H0 채택 등)
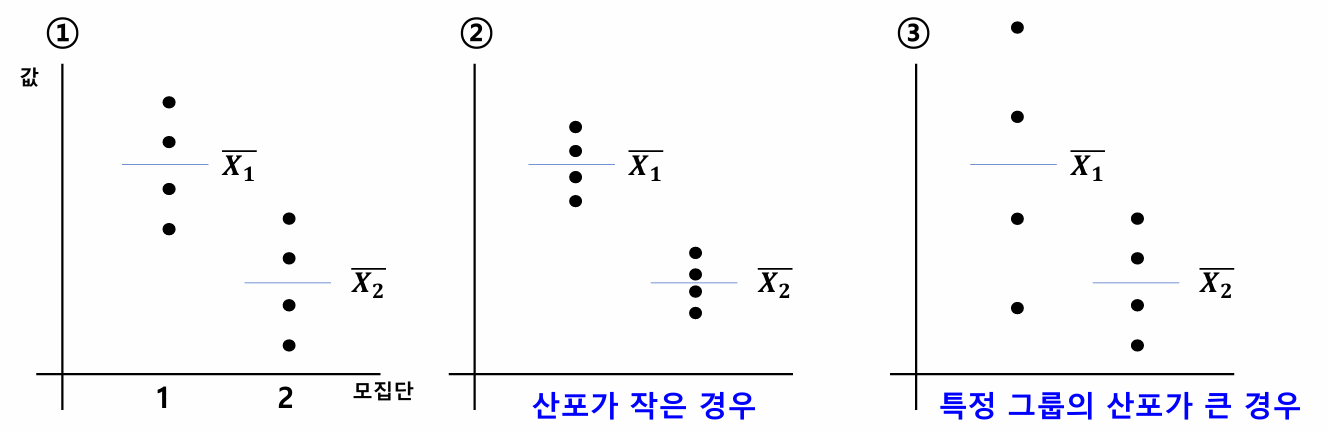
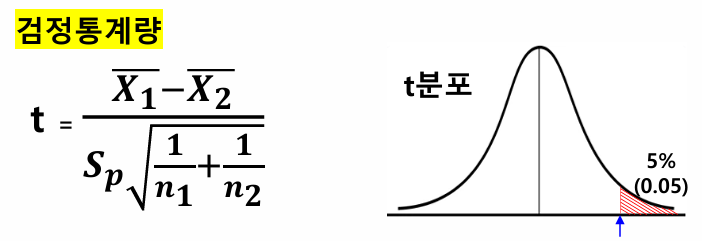
검정통계량, p-value, H0 채택 여부 함께 생각해보기
1. 가설검정 - 모평균 비교(3개)
4. ANOVA(분산분석)
* ANOVA는 Analysis of Variance로 F분포 활용
stats.f_oneway(a, b, c) (정규성O, 등분산성O 가정)
핵심 Concept
F = 그룹간 변동(분산) / 그룹내 변동(분산)
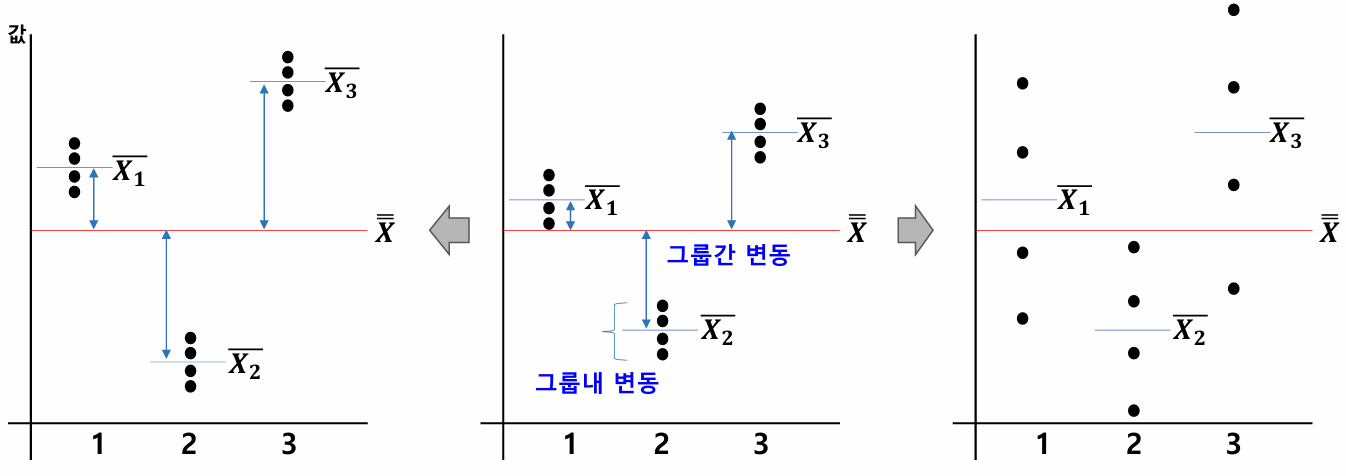
Q. 검정통계량 F값의 변화는 어떤 의미를 가질까?
가설설정
H0 : μ1 = μ2 = μ3
H1 : not H0 (적어도 하나는 같지 않다)
검정통계량
F = 그룹간 변동(분산) / 그룹내 변동(분산)
F값이 커진다는 건
1. 그룹간 변동이 커지거나
2. 그룹내 변동이 작아지거나
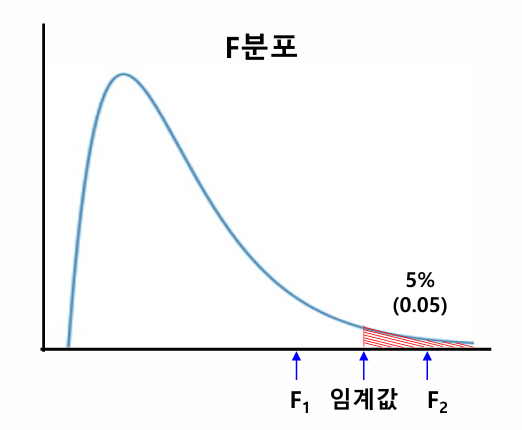
1. 검정통계량(F) 값이 증가하면 p-value 값은 작아짐
2. 검정통계량(F) 값이 증가하면 H0 기각
이번 강의에서는 모평균을 검정할 수 있는 여러가지 방법에 대한 이해와 각기다른 특징들을 설명해 주었다.
특히 산포에 대한 그림을 이용하여 수강자들의 쉬운 이해를 도왔다.
24년 빅분기 (필기+실기 Python) 최단기 합격패스
www.metacodes.co.kr
'[데이터자격시험용-필수요약정리]' 카테고리의 다른 글
| [2024 빅분기 실기] 메타코드 강의 후기 | 3유형 (5) - 상관분석 (0) | 2024.06.19 |
|---|---|
| [2024 빅분기 실기] 메타코드 강의 후기 | 3유형 (4) - 카이제곱검정 (0) | 2024.06.18 |
| [2024 빅분기 실기] 메타코드 강의 후기 | 3유형 (2) (0) | 2024.06.16 |
| [2024 빅분기 실기] 메타코드 강의 후기 | 3유형 (1) (2) | 2024.06.16 |
| 빅데이터 분석기획 - 데이터수집 및 저장계획 (0) | 2024.04.02 |