3. 포아송분포
- 단위시간/공간 내 발생하는 사건의 횟수를 확률변수 X라고 할 때
(발생 빈도가 낮은 사건)
- X~P(λ)으로 표기
- 포아송 분포의 확률함수
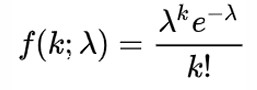
기댓값과 분산
- E(X) = λ
- Var(X) = λ
2. 연속확률분포
- 종류 : 정규분포, 표준정규분포, 균일분포, t-분포, X^2분포, F-분포, 감마분포, 지수분포
1. 정규분포

- 가우스 분포라고 부르기도 함
- 종 모양의 좌우대칭 분포
- 평균, 중앙값, 최빈값이 같음
- 평균이 μ, 분산이 σ², 표준편차 σ
- 위치는 평균이, 모양은 표준편차가 결정
- 첨도 3, 왜도 0

2. 표준정규분포
N(0,1)
- 평균이 0, 분산이 1인 정규분포
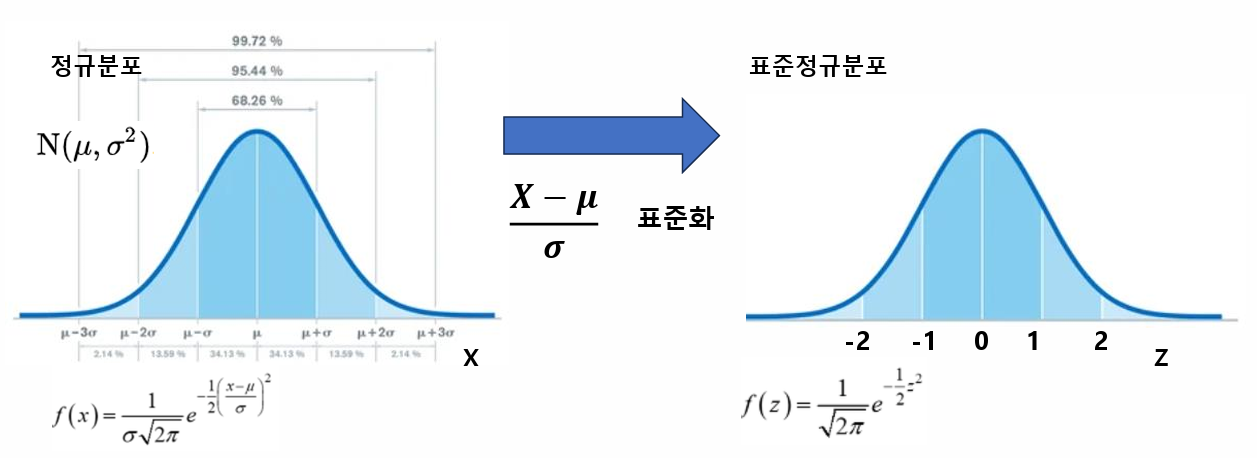
* 정규분포의 확률 계산(아래 면적)
- 정규분포를 표준화하여 표준정규분포로 만든다.
- 표준정규분포표를 보고 면적을 구한다. (주의사항 : Z분포표가 어느 구간을 나타내는지 확인할 것)

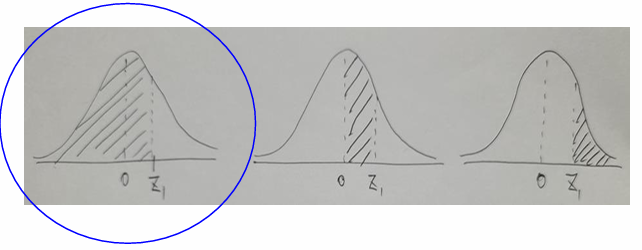
3. 균일분포
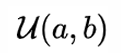
- 확률변수가 정의되는 구간에서 확률밀도함수 값이 모두 동일한 확률분포

아래 면적이 1이기 때문에 높이는 1/(b-a) 가 된다.
(b-a)*높이 = 1
4. t-분포
- 표본평균(x̄)으로 μ를 추정할 때 활용(모집단의 분산을 알지 못할 때)
- 표준정규분포와 같이 0에서 좌우 대칭이지만, 표준정규분포보다 긴 꼬리를 갖는다.
- 표본크기가 30 이상이 되면 정규분포에 근사한다.
5. χ²-분포(카이스퀘어 분포)
- 표본분산으로 모분산을 추정할 때 사용
- 적합도 검정(집단 1개가 특정 분포를 따르는지),
독립성 검정(두 범주형 변수가 서로 독립인지),
동일성 검정(두 집단 간에 각 범주에 속할 비율이 같은지)
6. F-분포
- 두 정규모집단의 분산을 비교하는데 활용
- 회귀분석, 3개 집단 이상의 평균을 비교하는데 활용
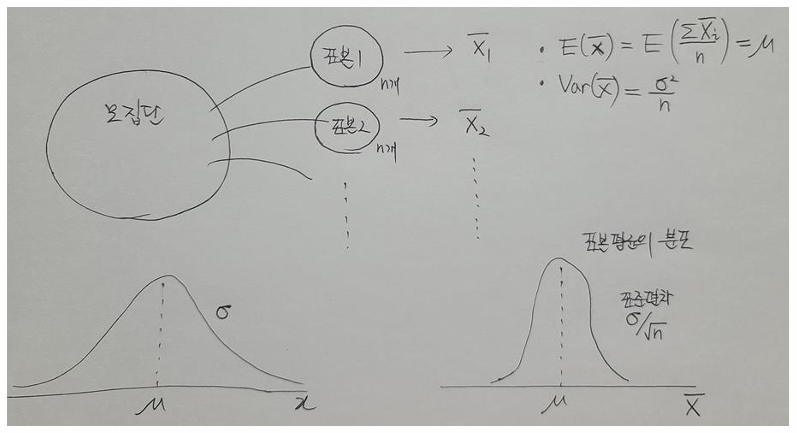
표본분포
- 한 모집단에서 일정한 크기로 표본을 뽑았을 때, 모든 표본에서 통계량을 계산할 때 이 통계량이 이루는 확률분포를
표본분포(Sample Distribution)라고 한다.
- 표본평균( x̄ )의 평균, 표준편차

'[데이터자격시험용-필수요약정리]' 카테고리의 다른 글
| 빅데이터 탐색 - 통계기법이해(가설검정) (0) | 2024.04.01 |
|---|---|
| 빅데이터 탐색 - 통계기법이해(중심극한정리/추정) (1) | 2024.04.01 |
| 빅데이터 탐색 - 통계기법이해(확률변수/이산확률분포/베르누이실행) (0) | 2024.03.31 |
| 빅데이터 탐색 - 통계기법이해(사건/확률/베이즈정리) (0) | 2024.03.31 |
| 빅데이터 탐색 - 통계기법이해(확률표본과 비확률표본/데이터의 중심) (0) | 2024.03.31 |