9. 확률변수 : 표본공간이 정의역, 실수값이 치역인 함수


10. 확률분포
- 확률변수의 값과 확률을 대응시켜 표나 그래프로 표현한 것

* 확률의 합은 1
11. 이산확률변수/연속확률변수 : 확률변수의 확률함수를 알고 있다면 사건이 일어날 확률을 계산할 수 있다.
- 이산확률변수 : 이산점에서 0이 아닌 확률값을 가지는 확률변수
- 연속확률변수 : 특정 실수 구간에서 0이 아닌 확률값을 가지는 확률변수




12. 확률변수의 기댓값(평균)
1. 이산확률변수

2. 연속확률변수

기댓값의 성질(X,Y는 확률변수, a,b는 상수)
- E(a) = a
- E(aX+b) = aE(X) + b
- E(aX+bY) = aE(X) + bE(Y)
13. 확률변수의 분산과 표준편차
- 분산 : 편차제곱 (X- μ )^2 의 기댓값(평균)
Var(X) = E((X- μ )^2)
1. 이산확률변수

2. 연속확률변수

분산의 성질(X,Y는 확률변수, a,b는 상수)
- V(a) = 0
- V(aX+b) = a^2V(X)
- V(aX+bY) = a^2V(X) + b^2V(Y) (단, X와 Y가 독립일 때)
표준편차 성질(X,Y는 확률변수, a,b는 상수)
- σ(a) = 0
- σ(aX+b) = aσ(X)
확률분포
1. 이산확률분포
- 종류 : 베르누이 확률분포, 이항분포, 포아송분포, 초기하분포, 음이항분포, 다항분포
1. 베르누이 확률분포(베르누이 시행)
- 각 실험에서 발생 가능한 경우의 수 2가지
ex) (성공,실패), (앞면,뒷면)
- 각 실험이 독립적으로 수행
- 모든 실험에서 결과의 확률이 동일
- 성공할 확률이 p인 경우 X~B(p)로 표기
X = 1(성공) or 0(실패)
P(X=1) = P(성공) = p
P(X=0) = P(실패) = 1-p
기댓값과 분산
- E(X) = p
- Var(X) = p(1-p) = pq
*q = 1-p
2. 이항분포
- 성공할 확률이 p인 베르누이 시행을 n번 반복했을 때 성공횟수(X)의 분포
X~B(n,p)로 표기 (n은 시행횟수, p는 성공할 확률)
이항확률분포의 확률질량함수(베르누이 시행을 n번 반복했을 때 x번 성공할 확률)
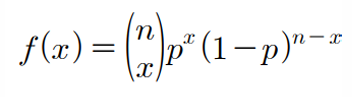
기댓값과 분산
- E(X) = np
- Var(X) = np(1-p) = npq
*q = 1-p
'[데이터자격시험용-필수요약정리]' 카테고리의 다른 글
| 빅데이터 탐색 - 통계기법이해(중심극한정리/추정) (1) | 2024.04.01 |
|---|---|
| 빅데이터 탐색 - 통계기법이해(포아송분포/정규분포/균일분포/표본분포) (4) | 2024.04.01 |
| 빅데이터 탐색 - 통계기법이해(사건/확률/베이즈정리) (0) | 2024.03.31 |
| 빅데이터 탐색 - 통계기법이해(확률표본과 비확률표본/데이터의 중심) (0) | 2024.03.31 |
| 빅데이터 탐색 - 통계기법이해(표본추출 방법) (0) | 2024.03.31 |